Deep learning exploded last year with the launch of ChatGPT. Large language models, specifically, have eaten up our arXiv papers, Twitter feeds, workflows, and lawmakers. But how do they actually work? What even is a transformer? Why is attention all you need? I feel that the subject, even in machine learning courses in many colleges, isn’t taught super well at all — mostly highlighting mathematical or implementation details. For this article, I’d like to explore an intuitive explanation of everything LLM: from transformers, to attention, architectures, and why context matters. You only need a base conceptual understanding of deep learning (gradients, backpropagation, dense layers, etc) to read, and by the end, I hope I can elucidate some of your latent curiosity. Many of these sections require knowledge from subsequent sections to fully grasp, so except to give it more than one read. I promise it’s worth it.

First, what’s a transformer?

The transformer, at its core, is simply a neural network architecture. It was first introduced in the infamous Attention is All You Need paper in 2017, for use in sequence to sequence (AKA seq2seq) tasks. These tasks include image to text, text to text, machine translation (language to language), and many other tasks. Hence, we see why it’s so aptly named: it “transforms” one sequence to another! At its inception, it outperformed the incumbent sequence modeling architectures, achieving state-of-the-art accuracy with ease. We’ll cover how it does this soon.

In addition to its accuracy, the transformer’s popularity and success can also be contributed to another factor: parallelization during training. Let’s consider other sequence modeling architectures (in your head, you should equate sequence modeling = language modeling in LLMs, as language itself is a innately sequence). Most common is the RNN and its variants (LSTM, GRU, etc). During training, an RNN must process text sequentially due to its time-dependent architecture, stepping over each word one or a few at a time. This is highly inefficient, especially if you have a large corpus of text. Even if you use a 1-dimensional CNN to process text, the convolution operation must step sequentially through the text; this is no faster. A transformer, on the other hand, can process all text in a given batch at once, in a parallel manner. There are no time steps need, so we aren’t slowed down by sequentially processing each word one by one. Researchers were quick to assess that this process can be distributed across many distributed computing systems commonly GPUs, to train on massive amounts of text efficiently. Thus, LLMs were naturally born out of the architecture. But what allows the transformer to process sequence data in parallel? What do I mean by “process”? To understand, we must first examine the transformer’s architecture.

The anatomy of a transformer.

The transformer’s architecture itself consists of a few layers, and some more advanced techniques to achieve the best performance. Let’s take a look at the architecture presented in the original paper:Attention is All You Need (2017) Transformer Architecture. On the left, we see an encoder block, and on the right, we see a decoder block. This depicts an encoder-decoder transformer architecture.

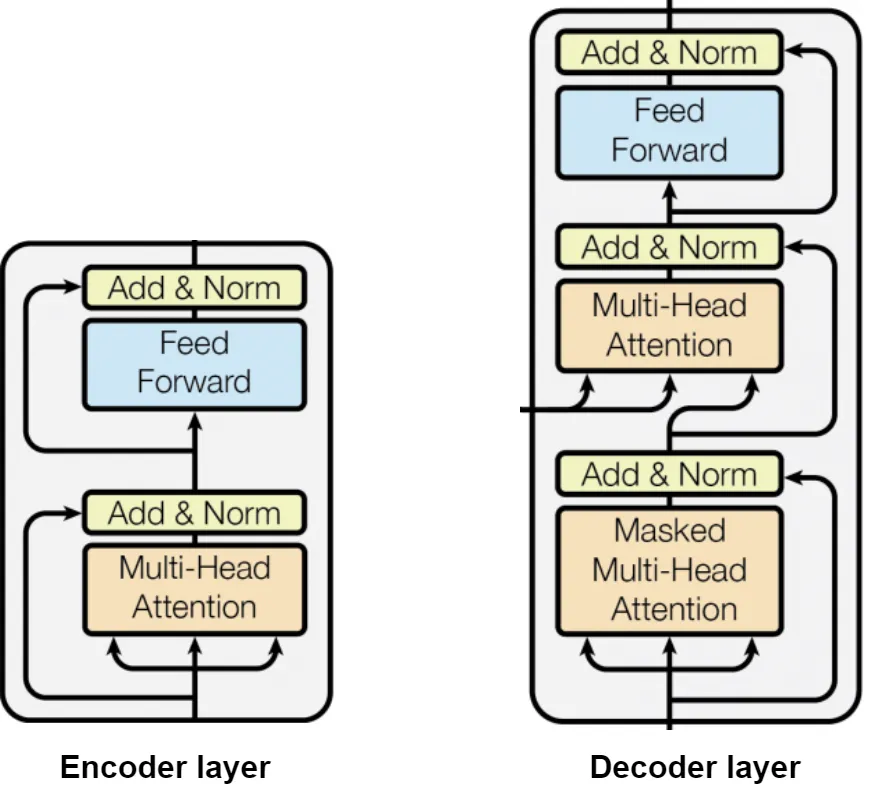
The architecture you see above consists of two primary parts: an encoder block and a decoder block. The encoder block is on the left-hand side, and the decoder block is on the right-hand side. The difference between the encoder and decoder is subtle, and we’ll cover it in a later section, but for now, just know that a typical transformer network implementation will consist of multiple encoder and decoder blocks stacked on top of each other, with the output of one block being the input to the next block.To understand the parts let’s examine only one of them for now; direct your eyes to the left side and note the different parts (keep in mind: both an encoder and a decoder have these parts, but they’re just used differently, which we’ll get to later).

1. Inputs: the inputs to the model is the data of whatever sequence you’re trying to train a model on! In language models, this is raw text. Transformers can also be used for other kinds of sequential data as well, so in those cases, you could input a pixel stream, audio data, video frames, time-series information, or other kinds of raw sequential data. For the rest of this section however, we will only focus on text processing.

2. Input Embedding: the inputs are then embedded into a rich representation. An embedding is actually its own model: typically, this model is pre-trained to learn a representation of words as vectors, where semantically similar words are closer to each other in some N-dimensional space. There are many kinds of embedding models, but they all work similarly. For example, the vectors representing “lizard” and “gecko” will be very close to one another in the N-dimensional vector space, but very far from the “motorcycle” vector. You can learn more about embeddings here, but in general you can think of an embedding as a general, learned, and global representation of words that a neural network can interpret mathematically.

3. Positional Encoding: once the input text are embedded, we need to give our transformer some way of understanding the position of the words in relation to one another. Remember, in other text models, such as an RNN, we understand word position implicitly since we go through our words one by one with each time step, which bakes it into the model. Transformers, on the other hand, since they process all input text simultaneously, do not inherently know about word position; only about what words are present in a body of text. Thus, for each word embedding, we concatenate a “position vector” to it, which contains the information about where the word is in a body of input text. There are many ways of generating this position vector, which I won’t cover here, but you can read about them here.

4. Attention: the attention layer is the most novel and important, part of the transformer, and is almost entirely responsible for why the whole architecture works so well! The attention layer, given an embedded body of text, is able to pick out the relevant words and “highlight” them in the model, while diminishing the irrelevant words, to create a rich representation of text just as a human would. Importantly, the attention mechanism learns about and represents word relations, or what words are most or least related to what other words. For example, in the sentence “the chair is blue”, the attention mechanism would be able to pick out that “chair” correlates highly to “blue”, but “the” does not correlate much with “blue”. Such a representation is valuable, as it increases the quality of data we use to generate sequences of text later in the transformer architecture. This is a very high-level overview of what attention is — the entire next section of this article is dedicated to explaining the intuition, as well as mathematical explanation, for why and how this works so well.

5. Residual Connection: you may notice that there’s no “residual connection” layer in the architecture above. This layer is the “add” part of “add and norm”, but is most commonly referred to as a residual connection. In any residual layer, it means adding (not concatenating!) the input of a layer to its output. Mathematically, if we use a residual connection after a layer f, instead of a standard x → f(x) transformation, we see x → f(x) + x. With a residual connection here, instead of F learning to predict f(x) as an input to the next layer, it essentially learns to predict the residual, or abs(f(x)-x), the difference between the layer f’s output and its input, as the best input to the next layer. This seems strange at first, but we do this for a few reasons. First is more intuitive: by adding the layer’s input to its output, the model is better at remembering its inputs in the long run across many layers and blocks, which inherently leads to better predictions. Second, and arguably more important, is that it reduces the vanishing gradient problem during training. Without a residual connection, it’s possible that f(x), and thus grad(f(x)), become increasingly small over time, leading to a stall or halt in learning. However, since we add the input x to f(x) in a residual connection, the smallest that f(x) + x can ever get is x. Naturally, since our inputs are non-vanishing in size (they’re always significant in size since they start large in the initial input embedding, which is then added to the first residual, then next, etc), this allows a permanent path for our gradients to flow through at least x between each layer during backpropagation without any vanish occurring. Thus, we see the value in having residual connections!

6. Layer Normalization: this is the “norm” part of “add and norm”. The output of the layer is normalized to a consistent distribuion (EX: a mean of zero and standard deviation of one to match a standard normal distribution). This process stabilizes training by reducing the covariate shift between layers. This shift occurs when the outputs of each layer converge to different distributions than the input data and other layers. By mitigating this shift, we allow the model to train “smoother”, since it learns to only process information found in a one generally consistent distribution. If the model were to try and predict over many different input distributions at each layer, the training process would likely be noisy, and the weights space of the model would be partly spent trying to account for these shifts rather than learning how to model language!

7. Feed Forward: this is just your typical dense/linear layer, or typically, a stack of many. It serves the same purpose than any other feed forward layer would, like adding non-linearity, transforming data to a new space, enriching the data, etc.

Thus, we see what composes one transformer block! When a transformer “processes” text, it’s flowing the data through many of these transformer blocks in the above order. When the data reaches the end of the transformer block stack, the output is theoretically a highly rich representation of our text we want to generate, based on our input data! there are two more steps before we can get output text (still assume text2text for this example):

1. Linear Layer: this linear layer serves a similar purpose as the feed forward layer in a transformer block, yet primarily just transforms the representation from the transformer stack into the same dimension as our vocabulary dictionary.

2. Softmax: the softmax function allows us to compute probabilities over our entire vocabulary dictionary, now that our data is the same size! At inference time, we select the token to generate next based on which probability is highest. A token is a word, punctuation, prefix, suffix, number, or anything else depending on how you embed and tokenize your text.

So with all the architecture figured out, how can we generate new text? Transformers use autoregressive generation to generate new text! This process is quite conceptually simple. Say that I want to generate text starting with “I am a”. First, I’d feed “I am a” into the model, which generates the output token via softmax as “happy”. Then, to generate the next token, “I am a happy” is fed into the model, which generates “person”. This process continues until the model deems the response is complete, usually with an EOS (end of sentence) token. Great! Now you know how a transformer is created. Now let’s delve into the secret sauce.

All you need to know about attention!

As we touched on earlier, the attention mechanism is the brains of the transformer. It allows the model to develop an intuition for what words relate to each other, where they are in a sentence, and how to use them to generate new text. Together with a positional encoding, we can learn long-range dependencies between words and different parts of a text input. Ultimately, attention will output an even richer vector representation of your input text for use downstream. You may remember from earlier that one step in the architecture is an embedding. If we already embed our text, why do we need attention? Good question. A text embedding captures global, semantic representations of words (EX: “king” and “queen” are semantically similar). Attention, on the other hand, captures the meaning and relation of words in context, as in within a body of text or sentence itself, as in our earlier “the chair is blue” example. So how does attention work? Let’s look at the formula:

The attention equation and formula!

I know, this looks scary, but this is how attention adds “context” to a body of text mathematically. We’ll break it down soon. For now, I’d like to point out the Q, K, and V variables. These stand for query, key, and value. These matrices each represent a different part of attention, and serve a different purpose. The query matrix represents the queries (text embeddings we want to generate with) we match against the keys. The key matrix represents what we want to generate from, or the embeddings the queries are compared against to determine relevance. The value matrix contains the actual content that the query-key matching process will retrieve from.

To calculate Q, K, and V, we need three new learned weights matrices, each of which is multiplied by the input to achieve Q, K, and V. Thus, we can rewrite attention as the following:

Self-Attention in terms of our learned weights matrices and inputs.

Note the similarities here, and how we calculate Q, K, and V. Here, consider X as the input to attention mechanism (embedded text with positional encoding or the output of the previous transformer block). This expansion makes it easier to view the runtime of the attention mechanism, which is quadratic to input, or O(n²). If you’re thinking this is computationally expensive, then you’re right! There is a lot of ongoing research on sub-quadratic sequence modeling architectures, such as S4 and Mamba, but nothing has stuck quite yet as an equally accurate, yet computationally more efficient, alternative.

This is a special case of attention called self-attention, since every input to calculate Q, K, and V is the same X! This equation makes more intuitive sense to me that the former, and I’d like to credit it here. Let’s break down what’s going on here, step by step:

1. This is the dot product of the key matrix with the query matrix. Mathematically, it represents how similar each query is with each key. For each query (which, remember, is a word embedding transformed by a learned matrix), a similarity score is computed for how similar it is to each key (which is also another word embedding transformed by a different learned matrix). You can think of the output of this step as a table with all the queries as the rows, the keys as the columns, and all values being numerical representing similarity.

2. This term represent a scaling factor by the square root of the dimension of the keys matrix. You may notice that both the query and key matrix must be the same dimension, and you’d be correct! This scaling prevents the similarity scores from growing too large in size, which would make the transformer’s mathematical operations at scale more inefficient.

3. In the resulting similarity score matrix, applying the softmax function makes each row of the matrix sum to one. Like any softmax operation, this means we can interpret each row with value x as the following probabilities: “this query is x% similar to this key”. This naturally enhances larger similarity scores, and diminishes smaller ones. Thus, we see that applying softmax is the logical operation that determines which keys the queries “pay attention to” versus not, and how much! The output of the softmax operation on our similarity score matrix is often displayed in research to visualize attention itself, and you may recognize a table like the following:Self-Attention similarity score matrix example after softmax. From https://theaisummer.com/attention/.

Now let’s look at the last step, which concludes our mathematical explanation of attention!

4. Recall how the value matrix, V, contains the actual content that will be retrieved using our similarity matrix calculated previously. Here, I believe that the term masking is a better fit than retrieve. You can also think of V as containing the actual information that we want to sequence, or “transform”. By multiplying our attention similarities and the value matrix, we retain the values that matter the most, and mask out the values that don’t matter at all (remember these were diminished mathematically by softmax), resulting in a rich vector representation of what information matters and what information doesn’t matter that can be used later for calculations and generation.

What I’ve just described is how to calculate attention with a single set of learned Q, K, and V weights matrices. This is known as single-head attention. However, in practice, this is not how we compute attention. A technique called multi-head attention is much more accurate and popular. In multi-head attention, we randomly initialize many sets of Q, K, and V weights matrices, which are all learned independently of one another. Each set of independent QKV weights matrices is known as a head. In multi-head attention, once each head computes its attention, they are all concatenated together as the output of the layer, ready to be fed into the next layer. Since each head’s weights are randomly initialized, they learn how to “attend” to different parts of the text in different ways, which is analogous to different humans reasoning about a sentence in their own unique way, creating a much more rich representation of the text.Visualization of self-attention! Visualization credits: https://github.com/jessevig/bertviz.

Congrats! You now know how we compute self-attention in seq2seq models. However, self-attention only is relevant if you’re dealing with data of the same modality. What if you’re trying to train a seq2seq model between different modalities, like translating from French to English, generating a caption from an image, or generating an image from an audio file? This is where we use cross-attention. Cross attention is only used in encoder-decoder architectures, which we’ll cover in the next section. The formula for cross-attention is as follows:Formula for Cross-Attention, expanded from QKV notation.

To understand this, we must revise our definition of X slightly. In practice, X is actually the output of the encoder block, and Y is the input to the decoder block (often the previous decoder output). Recall our definition of the query: the embeddings we want to generate with. In cross-attention, the query is comprised of your ending modality. Let’s focus on translation to highlight this. If I want to translate from English to French, my queries will be my French representations (autoregressively generated by the decoder), and my keys and values will be my English representations (from the encoder)! We’ll cover the difference between the encoder and decoder soon, I promise. First, let’s see how cross-attention is visualized:Visualization of Cross-Attention from French to English translation. Sourced from https://theaisummer.com/attention/.

So now you can see a little better how we use the query to continue generation in our second modality, and the key and value to guide the generation from our first modality. Hopefully, the intuition behind cross-attention can elucidate how self-attention works. It just so happens that self-attention is a special case of cross-attention, where X=Y. Now, we can finally cover encoders versus decoders.

Encoders and decoders: many architecture choices!

To understand encoders and decoders, we should discuss what each of them does, and some common architectures, use cases, and details about each. An encoder simply creates a representation of an input sequence as a vector, that only machines can interpret. A decoder is able to generate a new sequence given an input sequence. Both of them still use the same transformer architecture, with the attention mechanism; the difference lies in what we process and how we use the outputs of the transformer block. We can visualize this separation from our earlier architecture below:

Transformer encoder and decoder have the same architecture!

To further understand this, let’s go over a few different permutations of encoders and decoders in real-life transformer system implementations.

1. Encoder-Only Transformer: this type of transformer only consists of many encoder layers, with decoders entirely absent. This highlights the primary purpose of the encoder: to understand, but not generate, an input sequence. The output of an encoder-only transformer is nothing but a vector containing extremely rich information that encodes the input data’s meaning very well. Without both an encoder and decoder, this model can only use self-attention to reason about its inputs. This model is used exclusively for non-generative tasks, such as PoS tagging, NER, sentiment analysis, and others. Since the model’s output is only a representation of text, to perform anything with the encoder-only transformer, we must train an MLP (or dense) layer on top of it to transform the embedding into a desired discrete output space. A great example of a transformer using this architecture is BERT and its derivatives, which are commonly fine-tuned for many different tasks. This is even one project assigned in Brown’s CS1460.

2. Decoder-Only Transformer

   : this flavor only uses decoder layers. Again, since it only consists of one type of layer, it too can only utilize self-attention. Further, since we only use a decoder here, we can only generate a sequence given an input sequence. We generate this text autoregressively. As a symptom of this autoregression, the phenomena of right-shift is present. This occurs because the generated tokens are used to generate the next tokens, so our attention continually “shifts right” over time to fit these new tokens. This is the most popular architecture with LLMs, powering all of OpenAI’s GPT models, Llama, Claude, Mistral, and almost every other state-of-the-art LLM. It’s unique in that the instruction for the task, unlike when an encoder is present, is also the input. This makes the architecture harder to fine tune and generate outputs you exactly desire, since there’s no way to bake in the set or instructions of output you want to the model.

3. Encoder-Decoder Transformer: as you may guess, this architecture uses both an encoder and a decoder, exactly as the original 2017 paper does! You can refer to the first figure in this article to see this. Each block consists of both an encoder and decoder, with cross-attention connecting them both. However, within both the decoder and encoder independently, self-attention is used until it comes time to connect them both. This architecture is typically used to reason between two different types, or modalities, of input sequences, but can also be used to convert between homogeneous types as well. Tasks can include image captioning, translation, or just simply text generation, and anything seq2seq. In fact, Google Translate is at least in part powered by this type of transformer. The encoder is trained to turn input data into an optimal format for the machine decoder to understand, and the decoder is trained to use this format to autoregressively generate the desired output sequence. Since the “understanding” and “generation” are in a sense separated here, there are many techniques, such as tagging, that can be used to control the output of the transformer, more so than a decoder-only architecture.

Until more architectures are invented, this exhausts our list. One final thing I’d like to cover in this article is context length. News has been buzzing about LLM context lengths as they continue to increase in size, and now that you’re armed with the knowledge to understand them, we should dive in. This is often, in my experience, left out of the technical discussion on LLMs, so hopefully you find this useful.

Context length!

A context length is the maximum size, denominated in tokens, that a sequence model can process and make sense of at a time. In the context of LLMs, context can be thought of as the following: “how many words can I give to the model before it can’t understand it?” For example, GPT4–128k means that the GPT4 model has a context length of 128,000 tokens. The amount of words this is may very depending on your tokenizer, but you can play with OpenAI’s here.

So why does context length matter? Simply put, the longer the context length, the more stuff you can give to the model for it to understand, and the more you can do with it. If attention scales perfectly over an entire long context length, then your model would simply be able to reason with more inputs! Who wouldn’t want that? In practice, however, this isn’t always the case. In general longer context length = better for reasoning over large sequences, or large bodies of text.

Great! How do we increase the context length of our models? After the model is trained, you can’t increase the context length without further training. There are techniques, such as chunking your inputs across multiple inferences (runs of a model), but these are artificial. Say you have a model with a 2k context length. This means that the model was trained to only use 2k tokens, at maximum, in its attention mechanism. In theory, you could submit an input with 100k tokens, but the model simply wouldn’t know how to reference the trailing 98k tokens, how to reason about them, or their purpose in the text. In practice, most LLM APIs don’t even allow queries beyond the context length, since it simply introduces unnecessary compute for a highly inaccurate or unreasonable response.

To increase context lengths, we must either re-train the model or fine-tune it to utilize more tokens at once during attention. Good models will be trained to use the entire length of context evenly, known as “utilizing the context window”. To train a model like this, there are many techniques, such as randomly splitting important data across the entire length (from front to middle to back) to use when generating text downstream, teaching the model to always look at each part of the context. Other techniques involved advanced positional encoding methods. Remember those? They matter!

Large context lengths are hard though. They scale poorly. If you remember, the attention mechanism is quadratic. If you want to double the context length of a model, you’d be performing four times the compute. As we continue doubling and doubling, you can imagine how this becomes highly inefficient and expensive. Large context lengths appear to be less of a technical challenge than a compute challenge. If this is interesting to you, you should read this great article I found all about increasing context!

In conclusion.

I hope you paid attention (haha get it)! It’s always great to nail down the foundations, and we at Cerebral Valley brushed up on our own knowledge in the process of writing this. Now, if you’re curious about implementation details, I’d highly recommend The Annotated Transformer or Karpathy’s GPT From Scratch. Enjoy!